Searching or traversing is really important when it comes to accessing data from a given data structure. There are different methods of traversing/searching elements within these data structures such as Graphs and Trees.

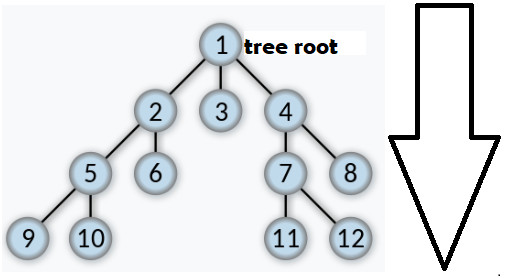
Breadth-first search is one example of these methods. BFS is an algorithm that traverses tree or graph and it starts from the tree root (the topmost node in a tree) or simply the top, and scans through all of the neighbour nodes at the current depth before moving on to the nodes/elements at the next depth level.

Simply put, BFS has to complete a layer, and move on to the next until there are no any layers left.

BFS uses the exact opposite workflow as depth-first-search, which goes the other way around.

A big difference in terms of the implementation between BFS and DFS is that BFS uses queues and DFS uses stacks.

Workflow of BFS

Implementation of BFS

There are two simple rules to follow when implementing BFS:

1. Visit every single element on a given layer
2. Move on to the next layer

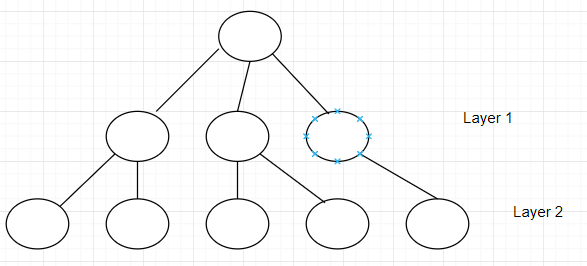
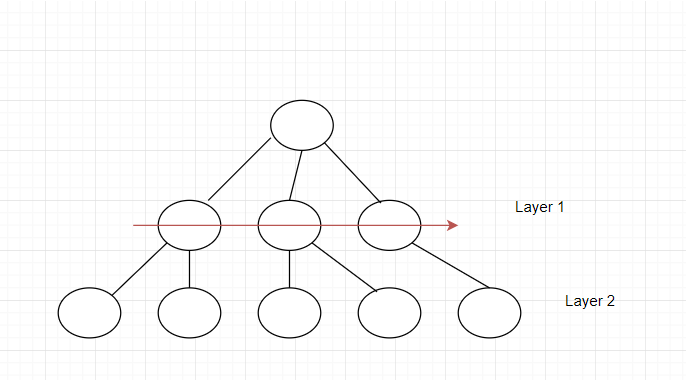
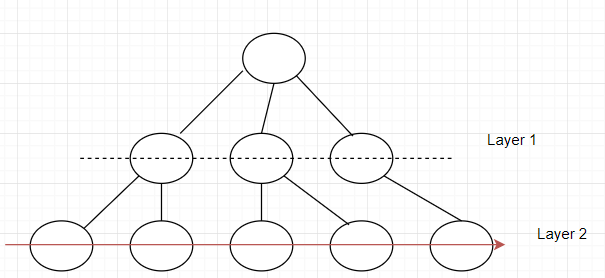
An example:

Before moving on to layer 2, layer 1 has to be gone through first.

After that, this is how it should be done:

Pseudocode

public void breadthFirstSearch(Graph G, Object S)
// G => Graph ; S => Source node
{
     define a queue named as Queue;
     insert the source node in the Q
     mark s as visited
     
     perform a while loop that keeps looping until the queue is not empty
        removing the current element from the queue as it will be visited now
        
        perform a for loop that goes through all neighbours of the current element
            if condition that checks if the current element/node/vertex is not visited
                if it has not been visited, enqueue it and mark it as visited
}

Actual code implementation

public void BFS(int s, int l) 
    { 
        // create an array that holds boolean values that will have length 'l'
        boolean visited[] = new boolean[l]; 
  
        // create a queue
        LinkedList<Integer> q = new LinkedList<Integer>(); 
  
        // mark the current node as visited and add it to the queue
        visited[s]=true; 
        q.add(s); 
  
        while (q.size() != 0) 
        { 
            // dequeuing a vertex from queue 
            s = q.poll(); 
  
            // get all adjacent vertices of the dequeued vertex  if a adjacent has not 
            // been visited, then mark it visited and enqueue it 
            Iterator<Integer> k = adj[s].listIterator(); 
            while (k.hasNext()) 
            { 
                int j = k.next(); 
                if (!visited[j]) 
                { 
                    visited[j] = true; 
                    q.add(j); 
                } 
            } 
        } 
    }