Searching and/or traversing are equally important when it comes to accessing data from a given data structure in Java. Graphs and Trees are an example of data structures which can be searched and/or traversed using different methods.
Depth-first-search, DFS in short, starts with an unvisited node and starts selecting an adjacent node until there is not any left. After that “procedure”, you backtrack until there is another choice to pick a node, if there isn’t, then simply select another unvisited node.
Implementation using Stack
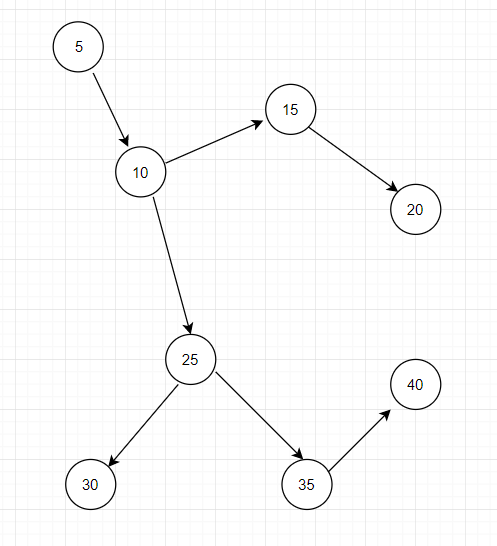
The order of the visited nodes for the picture above is: 5 10 25 30 35 40 15 20
Implementing DFS using the Stack data structure
Node.java represents each “ball” or “circle” on the graph above. It has a val which represents the “value” of each ball. It also has a boolean variable called visited which as the name suggests, it represents whether a Node has been visited by the traversal or not. The third instance variable Node class has is an ArrayList which represents all the adjacents (or neighbours) to the current node called adjacents. (If you want to know more about ArrayList, you can view this tutorial.)
In terms of methods in this class, there is a simple constructor that takes in a value and creates an empty ArrayList, and Setter and Getter methods and also a method that allows adding an adjacent Node.
Node.java
import java.util.*;
public class Node{
private int val;
private boolean visited;
private List<Node> adjecents;
public Node(int val) {
this.val = val;
this.adjecents = new ArrayList<>();
}
public void addAdjecents(Node n) {
this.adjecents.add(n);
}
public List<Node> getAdjacenets() {
return adjecents;
}
public int getVal() {
return this.val;
}
public boolean isVisited() {
return this.visited;
}
public void setVal(int v) {
this.val = v;
}
public void setVisited(boolean visited) {
this.visited = visited;
}
}
DFS.java
This class has only 1 method: the solution.
It uses Stack data structure and it takes Nodes as elements. It adds the specified element to the node and then marks it as visited. After that, there is a while loop that that keeps checking whether the stack is empty or not. If it isn’t, then remove one element from the stack, get the neighbours of the element that is being removed. Then, there is another loop, which purpose is to mark each neighbour node as visited and also it adds that neighbour node to the stack.
import java.util.*;
public class DFS {
public void stackSolution(Node node) {
Stack<Node> DFS_stack = new Stack<Node>();
DFS_stack.add(node);
node.setVisited(true);
while (!DFS_stack.isEmpty()) {
Node nodeRemove = DFS_stack.pop();
System.out.print(nodeRemove.getVal() + " ");
List<Node> adjs = nodeRemove.getAdjacenets();
for (int i = 0; i < adjs.size(); i++) {
Node currentNode = adjs.get(i);
if(currentNode != null && !currentNode.isVisited()) {
DFS_stack.add(currentNode);
currentNode.setVisited(true);
}
}
}
}
}
Main.java
In this class is the main method which creates 8 instances of the Node class and passes some values. (Keep in mind that this example below uses the graph above (the image). We are adding different nodes as neighbours to different nodes. After that, we start from node5 and traverse it.
import java.util.*;
public class Main {
public static void main(String [] args) {
Node node5 = new Node(5);
Node node10 = new Node(10);
Node node15 = new Node(15);
Node node20 = new Node(20);
Node node25 = new Node(25);
Node node30 = new Node(30);
Node node35 = new Node(35);
Node node40 = new Node(40);
node5.addAdjecents(node10);
node10.addAdjecents(node15);
node15.addAdjecents(node20);
node10.addAdjecents(node25);
node25.addAdjecents(node35);
node35.addAdjecents(node40);
node25.addAdjecents(node30);
DFS demo = new DFS();
System.out.println("DFS traversal of above graph: ");
demo.stackSolution(node5);
}
}
Output:
DFS traversal of above graph: 5 10 25 30 35 40 15 20